In the past ten years, topological insulators have emerged as a new exciting sub-field of condensed matter physics. As in an ordinary insulator, the highest occupied electronic band and the lowest empty band are separated by a bulk energy gap. However, the surface of a topological insulator has gapless states protected by time-reversal symmetry. This phenomenon is topological in the sense that certain fundamental properties, such as the number of gapless boundary modes, are insensitive to smooth changes in material parameters. Very recently, Kane and Lubensky have demonstrated that topological surface modes can also exist in mechanical systems by laying out the framework for a general theory of topological phonons in lattice on the edge of mechanical stability. Here we showed that these topological phonons can also exist, with a very rich phenomenology, in disordered materials such as jammed and quasi-crystalline systems.

topologically protected ZM and self stress The fact that disordered unit cells can be in different topological classes implies that there can be topologically protected boundary modes at the interface between two systems that have been connected in such a way so as to maintain the balance between constraints and degrees of freedom. Shown at the left is an example of an exponentially localized zero mode (blue) and a state of self-stress (yellow/purple) trapped at the interfaces between two topologically different unit cells (which have been periodically tiled for visual clarity and which have periodic boundary conditions along the edges).

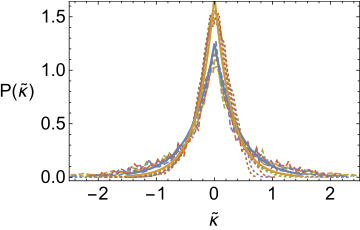distribution of penetration depths Prodded by questions about the nature of the jamming transition, we calculated the distribution of the exponential penetration depths characterizing these interfacial modes by averaging over many disordered configurations. We found that the distribution of decay lengths is itself approximately exponential, with the mean serving as a metric of the degree of randomness in the system. Furthermore, the distribution was only very weakly (logarithmically, in 2D) dependent on system size. This implies that for ever-larger jammed unit cells a smaller and smaller fraction of the surface zero modes (for systems in any topological class) are able to penetrate into the bulk.

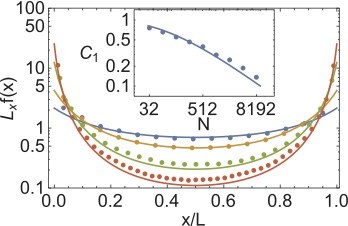zero modes in a strip This seemingly innocuous result impacts one of the cornerstone ideas about the nature of the jamming transition. In particular, a counting/variational argument has been used to explain why, among other things, the density of states of jammed systems has a constant plateau extending to zero frequency as the critical point is approached. However, this argument relies on a particular scaling bound for the value of the total amplitude of all of the surface zero modes penetrating into the sample. This scaling bound is inconsistent with the consequences of our characterization of the topological states, and indeed we find that with increasing system size the total amplitude of surface zero modes in the center of otherwise isostatic packings decays to zero too fast with system size for the variational argument to hold.