Kirigami
Kirigami
 The next decade promises to revolutionize the way we think about generating structures. Three-dimensional printing, with its ability to both prototype and create intricate structures as desired at low cost, is well on its way to technological maturity. Much less attention has been paid to a complementary idea: controllable two-dimensional surfaces that can self- assemble via simple cues into responsive three dimensional structures. Whereas 3D printing typically assembles heavy volume-filling elements, reduced-dimensionality objects can be both light yet extremely strong, as in a geodesic dome or the skeleton of a diatom. Moving forward both types of material design will be required, but less attention has been paid to the control of surfaces than to printing.
The next decade promises to revolutionize the way we think about generating structures. Three-dimensional printing, with its ability to both prototype and create intricate structures as desired at low cost, is well on its way to technological maturity. Much less attention has been paid to a complementary idea: controllable two-dimensional surfaces that can self- assemble via simple cues into responsive three dimensional structures. Whereas 3D printing typically assembles heavy volume-filling elements, reduced-dimensionality objects can be both light yet extremely strong, as in a geodesic dome or the skeleton of a diatom. Moving forward both types of material design will be required, but less attention has been paid to the control of surfaces than to printing.
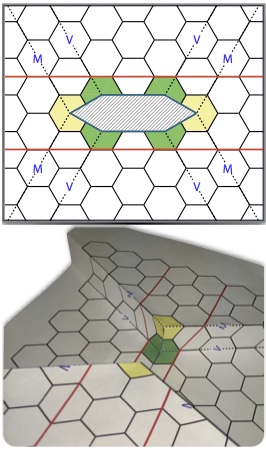
Origami has been much studied of late, but less so kirigami, a design paradigm that takes the folded paper of origami but also incorporates cutting (and possibly re-connecting) of the two-dimensional sheet. Removing sections of the paper allows one to imbed topological defects and easily program positive- and negative-gaussian-curvature points into the surface. This allows kirigami-based techniques to simply achieve certain target structures that would require highly complex pure origami designs, involving not only many additional folds but large swathes of “wasted” triple thickness paper.
 The difficulty, though, is in coming up with a set of rules to constrain the allowed kirigami cuts and folds to turn this idea into a useful tool for designing real 3D structures. Pop-up books can be thought of as kirigami, which highlights the rich, intricate structures that artists have been able to make. However, to solve the inverse problem of prescribing a set of cuts and folds to achieve a target structure algorithmically requires a less artistic approach.
The difficulty, though, is in coming up with a set of rules to constrain the allowed kirigami cuts and folds to turn this idea into a useful tool for designing real 3D structures. Pop-up books can be thought of as kirigami, which highlights the rich, intricate structures that artists have been able to make. However, to solve the inverse problem of prescribing a set of cuts and folds to achieve a target structure algorithmically requires a less artistic approach.
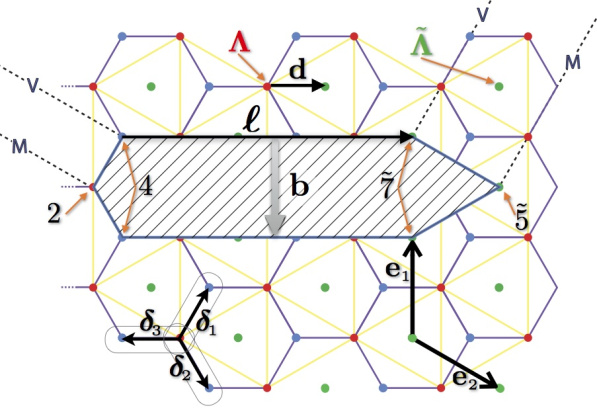
Transitioning from artistry to algorithm requires a systematic reduction in the types of allowed cuts. To that end, we considered starting from a honeycomb lattice — a natural choice if we are considering, e.g., graphene-like materials or fixed-edge-length structures with a minimum number of fixed-length-struts per unit area. We then determined the complete set of basic kirigami moves allowed under the condition that both the underlying triangular lattice of the nodes and the dual triangular lattice of the faces are preserved by any cuts made. We found that this restrictive version of kirigami is can be used to program a set of cuts and folds to create a stepped surface that mimics a desired target surface. Our current work involves relaxing some of the rules we imposed in order to explore the diversity of structures that can be achieved by only slightly bending the rules we proposed.