Anomalous interfaces in confluent cell models
Soft active living matter
The process of compartmentalizing different cell populations, and maintaining those boundaries, is of vital importance in processes ranging from early embryonic development to tumor metastasis. But how can dense biological tissue maintain sharp boundaries between coexisting cell populations? A common paradigm, the differential adhesion hypothesis, treats each cell population as an immiscible fluid and suggests that cell sorting and compartmentalization are driven by an effective surface tension. The precise cellular mechanisms that govern effective surface tension are still under debate; some investigations suggest it is dominated by adhesive interactions, while others implicate actomyosin contractility, or a co-regulation of these two effects. Indeed, it is not even clear that different methods for measuring the effective surface tension should yield consistent results, which could explain discrepancies between observations and lead to nontrivial and unexpected dynamics for cell sorting and compartmentalization.
 Here we present a possible explanation for these observations based only on the assumption that cells interact mechanically with touching neighbors, and that they might regulate these interactions differently with “unlike” cells. We focus on models for single layers of confluent cells — 2D Voronoi models — with no cellular gaps or overlaps.We include an additional interfacial tension between different cell types to mimic the mechanical changes that are known to occur at so-called “heterotypic” contacts. Surprisingly, we find that this model has a large discrepancy in different macroscopic measurements of the effective surface tension between coexisting cell populations.
Here we present a possible explanation for these observations based only on the assumption that cells interact mechanically with touching neighbors, and that they might regulate these interactions differently with “unlike” cells. We focus on models for single layers of confluent cells — 2D Voronoi models — with no cellular gaps or overlaps.We include an additional interfacial tension between different cell types to mimic the mechanical changes that are known to occur at so-called “heterotypic” contacts. Surprisingly, we find that this model has a large discrepancy in different macroscopic measurements of the effective surface tension between coexisting cell populations.
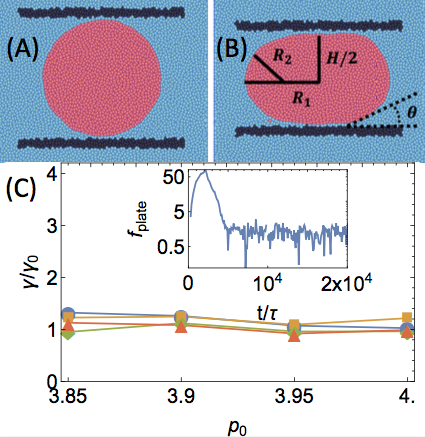
We first probe the effective surface tension of a cell droplet by numerically implementing a parallel-plate compression experiment, a popular technique in biological systems. This method measures surface tensions using only the geometry of a deformed droplet and the forces exerted, i.e., without needing to measure fluid viscosities. We find that the long-time limit of the forces needed to maintain droplets at a particular deformation corresponds to an effective interfacial tension matching the microscopic value we impose in the model.
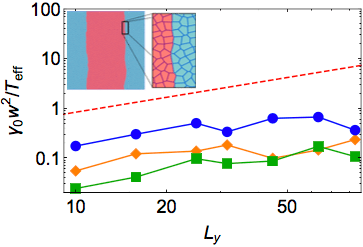 This, of course, is not surprising. However, we next probe the effective surface tension by measuring the spectrum of fluctuations at an interface. One common method of extracting the surface tension of a fluid phase boundary is to look at the structure and dynamics of capillary waves. In equilibrium simulations this is straightforward, as one can directly connect the interfacial roughness to the effective surface tension using standard techniques. We simulate our cells using both equilibrium (overdamped Brownian) and non-equilibrium (self-propelled particle) dynamics, and in both cases we find an interface that is orders of magnitude sharper than expected.
This, of course, is not surprising. However, we next probe the effective surface tension by measuring the spectrum of fluctuations at an interface. One common method of extracting the surface tension of a fluid phase boundary is to look at the structure and dynamics of capillary waves. In equilibrium simulations this is straightforward, as one can directly connect the interfacial roughness to the effective surface tension using standard techniques. We simulate our cells using both equilibrium (overdamped Brownian) and non-equilibrium (self-propelled particle) dynamics, and in both cases we find an interface that is orders of magnitude sharper than expected.
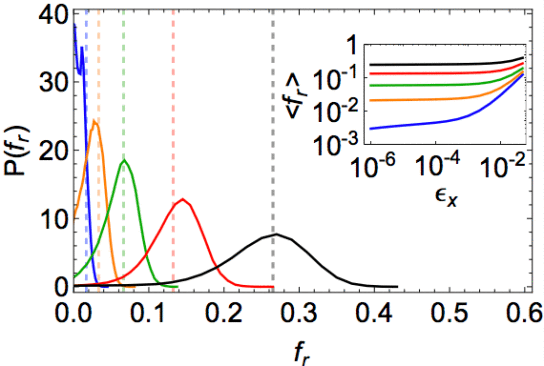 This reduction in the scale of interfacial fluctuations can be understood as a direct consequence of the topological nature of the interaction rules in these cell models. In particular, even though the energy is a continuous function as cell rearrange, there are discontinuous changes in the force whenever cells exchange neighbors. The topological (rather than strictly metric) interactions between cells lead to a cusp-like energy landscape, which in turn suppresses fluctuations, pinning cells to the boundary and sharply compartmentalizing the cells. A simple topological argument, in terms of particularly ordered Voronoi geometries, indeed predicts the major features of the distribution of restoring forces felt by cells at the interface.
This reduction in the scale of interfacial fluctuations can be understood as a direct consequence of the topological nature of the interaction rules in these cell models. In particular, even though the energy is a continuous function as cell rearrange, there are discontinuous changes in the force whenever cells exchange neighbors. The topological (rather than strictly metric) interactions between cells lead to a cusp-like energy landscape, which in turn suppresses fluctuations, pinning cells to the boundary and sharply compartmentalizing the cells. A simple topological argument, in terms of particularly ordered Voronoi geometries, indeed predicts the major features of the distribution of restoring forces felt by cells at the interface.
This interfacial sharpening mechanism has obvious implications for cell compartmentalization, but it also may influence the process of cell sorting. It is commonly assumed that both compartmentalizing and sorting proceed as if cells were immiscible fluids; we have seen that many-fold vertices may fundamentally alter compartmentalization, and we speculate that they may likewise have profound consequences for the process by which cells sort. Recent work has suggested that surprising consequences can arise from systems interacting via topological interactions rather than purely metric-based ones. While much of the work in this direction has focused on explicitly non-equilibrium systems — animal flocking or self-propelled particles interacting with combined Viscek and Voronoi dynamics — here we have shown that surprising interfacial behavior may arise as a generic consequence of the cusp-like landscape generated by the topological rules.