qTensorFunctions.h File Reference

#include "std_include.h"
#include "symmetric3x3Eigensolver.h"

Include dependency graph for qTensorFunctions.h:

This graph shows which files directly or indirectly include this file:

Macros
#define	HOSTDEVICE   inline __attribute__((always_inline))

Functions
HOSTDEVICE void	qTensorFromDirector (scalar3 n, scalar S0, dVec &q)
	return a qtensor given a director and a value of S0 More...
HOSTDEVICE scalar	TrQ2 (dVec &q)
	Tr(Q^2) = Q_{kl}Q_{lk}. More...
HOSTDEVICE scalar	TrQ3 (dVec &q)
	Tr(Q^3) More...
HOSTDEVICE scalar	TrQ2Squared (dVec &q)
	(Tr(Q^2))^2 More...
HOSTDEVICE dVec	derivativeTrQ2 (dVec &q)
	derivative of Tr(Q^2) w/r/t q[0] .. q[4] More...
HOSTDEVICE dVec	derivativeTrQ3 (dVec &q)
	derivative of Tr(Q^3) w/r/t q[0] .. q[4] More...
HOSTDEVICE dVec	derivativeTrQ2Squared (dVec &q)
	derivative of (Tr(Q^2))^2 w/r/t q[0] .. q[4] More...
HOSTDEVICE dVec	allPhaseComponentForces (dVec &q, scalar &a, scalar &b, scalar &c)
	Phase components combined into one for computational efficiency. More...
HOSTDEVICE dVec	QjkQki (dVec &q)
	Q_{jk}Q_{ki}. More...
HOSTDEVICE scalar	determinantOfQ (dVec &q)
	determinant of a qt matrix More...
HOSTDEVICE scalar	eigFromVecs (vector< scalar > &eVec, scalar ev0, scalar ev1, scalar ev2)
	eVec is Q*e, ev0,ev1,ev2 are components ofe More...
HOSTDEVICE void	eigensystemOfQ (dVec &q, vector< scalar > &eVals, vector< scalar > &eVec1, vector< scalar > &eVec2, vector< scalar > &eVec3)
	get the eigensystem associated with a Q tensor More...
HOSTDEVICE void	eigenvaluesOfQ (dVec &q, scalar &a, scalar &b, scalar &c)
	Get the eigenvalues of a real symmetric traceless 3x3 matrix. More...

Macro Definition Documentation

HOSTDEVICE

#define HOSTDEVICE   inline __attribute__((always_inline))

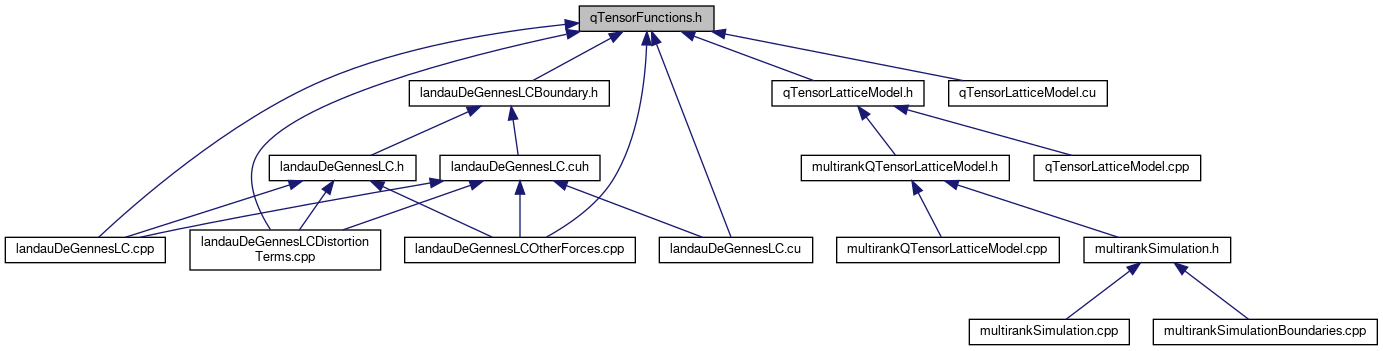
The Q-tensor has five independent components, which will get passed around in dVec structures... a dVec of q[0,1,2,3,4] corresponds to the symmetric traceless tensor laid out as (q[0] q[1] q[2] ) Q = (q[1] q[3] q[4] ) (q[2] q[4] -(q[0]+q[3]) )

This file implements handy manipulations and functions of the Q-tensor as laid out this way